SIMULASI DAN METODE MONTE CARLO
Kata “simulasi” dan istilah “Monte Carlo” mungkin sudah familiar bagi kita. Jika kita mendengar kata simulasi, secara otomatis ingatan kita biasanya akan tertuju pada perhitungan dalam beberapa percobaaan.
Jika kita mendengar istilah Monte Carlo, mungkin kita akan langsung teringat pada Monte Carlo Rally di Monaco atau Monte Carlo Casino di Las Vegas (yang merupakan asal dari munculnya istilah Monte Carlo), sedangkan Monte Carlo yang akan dibahas disini adalah Metode Monte Carlo dalam statistik, matematika dan aktuaria, atau bahkan fisika, yang mungkin terdengar agak asing di telinga kita. Simulasi adalah suatu percobaan yang biasanya dilakukan dengan menggunakan komputer, dan melibatkan bilangan acak. Bilangan acak tersebut adalah barisan dari variabel acak uniform yang saling bebas dalam interval [0,1).
Berikut adalah contoh dua kelompok situasi yang membuktikan simulasi sangat berguna. Situasi pertama, situasi pada kehidupan sehari-hari : “pemodelan arus pasien yang masuk rumah sakit”, dan “pemodelan evolusi dari epidemik pada waktu dan tempat tertentu”. Situasi kedua, situasi dalam menyelesaikan persoalan matematika: “test dalam hipotesis statistik”, dan “pricing option (derivatif ) pada aset keuangan”. Kedua situasi tersebut sulit untuk diselesaikan dengan menggunakan murni metode analitik. Situasi pertama merupakan stochastic, dan mungkin terdapat interaksi yang kompleks antara sumber daya manusia dengan bagian tertentu dari sistem, dan kesulitannya bertambah dengan syarat-syarat untuk menentukan strategi yang optimal.
Dalam situasi kedua, tentang hipotesis statistik, setelah memperoleh data dari investigasi statistik, nilai numerik dari beberapa statistik dapat dihitung, tetapi distribusi dari statistik tersebut dalam hipotesa nol yang sangat sulit sekali untuk diturunkan. Dan pada situasi kedua, tentang pricing option, permasalahan sering berujung pada perhitungan integral lipat yang tidak mungkin untuk diselesaikan dengan metode analitik ataupun metode numerik konvensional, namun integral tersebut dapat diestimasi dengan menggunakan metode Monte Carlo. Metode Monte Carlo adalah kelas algoritma komputasi yang luas yang mengandalkan random sampling untuk memperoleh hasil numerik. Metode ini sering digunakan dalam masalah fisika dan matematika dan yang paling cocok diterapkan ketika tidak mungkin untuk mendapatkan ekspresi closed-form atau tidak layak untuk diterapkan algoritma deterministik.
Metode Monte Carlo sering digunakan dalam tiga masalah berbeda: optimasi, integrasi numerik dan generasi sampel dari distribusi probabilitas. Penggunaannya untuk pemodelan dari fenomena dengan ketidakpastian yang signifikan dalam input, seperti perhitungan risiko dalam bisnis. Metode ini secara luas digunakan dalam matematika, misalnya untuk menghitung multi dimensi definite integral dengan syarat batas yang rumit. Ketika metode ini diterapkan dalam eksplorasi ruang angkasa dan eksplorasi minyak, hasil memprediksi metode ini atas kegagalan, biaya dan jadwal overruns secara rutin lebih baik daripada intuisi manusia atau metode alternatif yang lebih “soft”.
Versi modern dari metode Monte Carlo diciptakan pada tahun 1950-an oleh Stanislaw Ulam, ketika ia bekerja pada proyek senjata nuklir yang dipimpin oleh Nicholas Constantine Metropolis, bersama dengan John von Neumann di Los Alamos National Laboratory. Istilah Monte Carlo sendiri berasal dari Monte Carlo Casino, di mana paman dari Stanislaw Ulam biasa berjudi.
Secara umum, simulasi mungkin cocok suatu masalah yang sangat sulit untuk diselesaikan secara analitik. Statistik muncul dari sampling experiment (contohnya rata-rata sampel dan proporsi sampel) yang biasa digunakan untuk mengestimasi parameter yang menjadi perhatian dalam masalah dasar, sistem atau populasi.
Karena simulasi menghasilkan estimasi dari parameter yang menjadi perhatian, tentunya selalu akan terdapat error. Berikut ini contoh estimasi perhitungan definite integral.
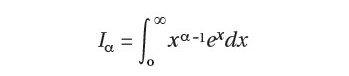
Untuk a konstanta riil positif. Jika X adalah variabel acak yang memiliki fungsi probabilitas densitas f pada [0,ºº) dimana f(x)=e- x, maka integral di atas dapat dituliskan dalam bentuk ekspektasi dari fungsi variabel acak sebagai berikut:
![]()
Sehingga estimasi statistik untuk integral Iª dapat diperoleh dengan melakukan sampling experiment yang terkontrol. Ambil sampel acak yaitu pengamatan X1, X2 , ..., Xn dari fungsi probabilitas densitas f. Kemudian definisikan statistik sebagai berikut:
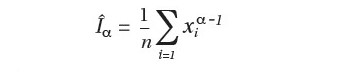
Jelas Ϊ adalah estimasi tak bias dari Iª dan asumsikan {Xi} saling bebas, variansi dari Ϊ diberikan sebagai berikut:
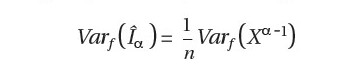
Maka deviasi standar untuk distribusi sampling dari statistik Ϊ adalah
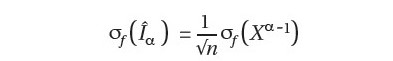
.jpg)
Istilah Monte Carlo dan simulasi cenderung digunakan bergantian dalam literatur. Disini simulasi didefinisikan sebagai percobaan yang terkontrol, biasanya menggunakan komputer, dengan bilangan acak dari distribusi uniform pada interval [0,1] yang saling bebas. Sedangkan metode Monte Carlo adalah metode untuk mengestimasi nilai dari suatu integral (atau sum) menggunakan nilai realisasi dari suatu simulasi. Metode ini mengeksploitasi hubungan antara integral (atau sum) dan ekspektasi dari suatu fungsi variabel acak.
(Reinfokus Edisi 1, Tahun 2013)
Author





 14084
14084



 04 Jan 2017
04 Jan 2017 53664 kali
53664 kali





