14 May 2019
5311
5311
Accounting & Finance
Principal tidak selalu sebesar 1 melainkan sebesar K > 0. Oleh sebab itu, dapat didefinisikan amount function A (t) yang memberikan accumulated value di waktu t ? 0 dari investasi tersebut. Amount function A (t) dapat ditulis sebagai berikut :
Tingkat Bunga Sederhana
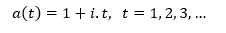
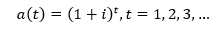
Nilai Sekarang
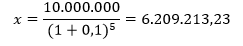
Simple Interest & Compound Intrest
Tingkat Bunga
Menurut Kellison (2009), bunga adalah kompensasi yang dibayarkan peminjam kepada yang meminjamkan. Keberadan bunga tersebut menimbulkan konsep time value of money. Konsep ini menjelaskan bahwa sejumlah uang pada waktu sekarang, akibat penerimaan bunga tertentu, nilainya tidak akan sama di masa depan/masa sebelumnya. Untuk memahami bunga lebih lanjut, berikut dijelaskan beberapa prinsip dasar dalam pengukuran bunga.
Accumulation dan Amount Function
Transaksi finansial yang sering dilakukan adalah investasi sejumlah uang. Pada proses investasi tersebut, sejumlah uang yang diinvestasikan disebut sebagai principal dan jumlah total uang yang diterima setelah beberapa waktu investasi disebut sebagai accumulated value. Selisih dari accumulated value dan principal disebut sebagai bunga yang diterima selama periode investasi.
Misal dilakukan investasi dengan principal sebesar 1, maka dapat didefinisikan accumulation function a(t) yang memberikan accumulated value di waktu t?0 dari investasi tersebut. Accumulation function tersebut memiliki beberapa sifat sebagai berikut :
1. a (0) = 1.
2. a (t) umumnya adalah fungsi yang naik atau tidak turun.
Hal tersebut ditunjukkan oleh jumlah total uang yang diinvestasikan selalu bertambah tiap waktunya.
3. Jika bunga naik secara kontinu, maka a (t) merupakan fungsi kontinu.
(Kellison, 2009)
Principal tidak selalu sebesar 1 melainkan sebesar K > 0. Oleh sebab itu, dapat didefinisikan amount function A (t) yang memberikan accumulated value di waktu t ? 0 dari investasi tersebut. Amount function A (t) dapat ditulis sebagai berikut :
Selanjutnya, jumlah bunga yang diperoleh pada periode investasi ke - n dinotasikan dengan In. Nilai In dapat ditulis sebagai berikut :
Tingkat Bunga Sederhana
Misal dilakukan investasi dengan principal sebesar 1 sedemikian sehingga jumlah bunga yang diperoleh setiap periodenya adalah konstan. Hal tersebut digambarkan dengan accumulated value sebesar 1 + i di akhir periode pertama, 1 + 2i di akhir periode kedua, dan seterusnya. Sehingga, secara umum, diperoleh accumulation function yang linier yaitu :
Persamaan tersebut merupakan accumulation function yang menggunakan tingkat bunga sederhana (Kellison, 2009).
Tingkat Bunga Majemuk
Misal dilakukan investasi dengan principal sebesar 1 sedemikian sehingga jumlah bunga yang diperoleh setiap periodenya diinvestasikan kembali pada periode berikutnya. Hal tersebut digambarkan dengan accumulated value sebesar 1 + i di akhir periode pertama. Nilai 1 + i dapat dianggap sebagai principal pada awal periode kedua sedemikian sehingga accumulated value di akhir periode kedua adalah sebesar (1+i) + i (1+i) = (1+i)2. Dan seterusnya, sehingga diperoleh :
Persamaan tersebut merupakan accumulation function yang menggunakan tingkat bunga majemuk (Kellison, 2009).
Nilai Sekarang
Berdasarkan kasus-kasus diatas, investor menginginkan sebaliknya yaitu investor ingin mengetahui seberapa besar principal yang diinvestasikan sedemikian sehingga accumulated value di akhir satu periode adalah sebesar 1. Dari pernyataan tersebut, didefinisikan discount factor v sebagai berikut :
Contoh :
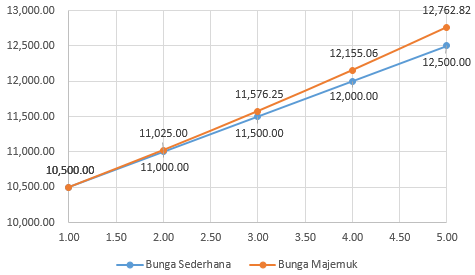
1. Mordekhai berinvestasi dengan principal sebesar Rp. 10.000,- dengan tingkat bunga tahunan i=5% selama 5 tahun. Hitung hasil investasi di setiap akhir tahun selama periode investasi berdasarkan tingkat bunga sederhana dan majemuk ?
2. Faisal ingin membeli motor 5 tahun yang akan datang di harga Rp. 5.000.000,- dengan berinvestasi senilai x pada tingkat bunga i = 10%. Tentukan nilai awal investasi x untuk membeli motor tersebut ?
Sumber :
Kellison, Stephen G. (2009). The Theory of interest, 3rd Edition. McGraw-Hill.
Cunningham, R.J., Herzog, T.N., & London, R.L. (2006). Models for Quantifying Risk. Winsted: ACTEX Publications.
Penulis
Iqbal Hediananda Putra, S.Si
Email: iqbal@indonesiare.co.idFollow Us
