Mengenal Geostatistics
Geostatistika merupakan aplikasi ilmu Statistika yang sangat berkembang dan berasal dari industri pertambangan. Ilmu ini pertama kali muncul pada awal tahun 1950 di Afrika Selatan oleh seorang Insinyur yang bernama DG Krige dan HS Sichel yang mempunyai latar belakang statistician. Selanjutnya konsep ini dikembangkan oleh seorang Insinyur berkebangsaan Perancis yang bernama Georges Matheron. Pada perkembangan saat ini, Geostatistika menggabungkan banyak metode, teori dan teknik agar mampu menyelesaikan permasalahan-permasalahan dalam konteks spasial (Wackernagel, 1995).
Secara umum pembahasan dalam Geostatistika dapat dibedakan menjadi tiga bagian yaitu Linier Stasioner Geostatistik, Linier Non Stasioner Geostatistik dan Non Linier Geostatistik. Pembahasan mengenai Linier Stasioner Geostatistik akan mengulas metode Univariate ataupun Multivariate yang berdasarkan kombinasi linier dari sampel yang diambil. Nilai-nilai dari sampel merupakan fungsi random dan diasumsikan stasioner atau tidak terpengaruh oleh trend tertentu. Jika nilai-nilai tersebut tidak stasioner maka dapat digunakan Non Stasioner Geostatistik. Kedua pembahasan sebelumnya mengasumsikan pendekatan linier sedangkan jika diperlukan pendekatan non linier maka dapat menggunakan Non Linier Geostatistik.
Analisa dalam Geostatistika membutuhkan data spasial yaitu data yang disajikan dalam posisi geografis dari suatu obyek yang berkaitan dengan lokasi, bentuk dan hubungan dengan ruang bumi. Penyajian data geografis dilakukan dengan menggunakan titik, garis dan luasan. Data spasial berupa data diskret atau kontinu dan dapat juga memiliki lokasi spasial beraturan (regular) maupun tak beraturan (irregular). Data spasial dikatakan mempunyai lokasi yang regular jika antara lokasi yang saling berdekatan satu sama lain mempunyai posisi yang beraturan dengan jarak yang sama besar. Sedangkan dikatakan irregular ketika lokasi yang saling berdekatan satu dengan yang lain mempunyai posisi yang tidak beraturan dengan jarak yang berbeda (Alfiana, 2010). Salah satu yang membedakan studi kasus spasial dengan studi lainnya yaitu data spasial memiliki kaitan dengan data lainnya pada suatu ruang atau daerah tertentu.
Berdasarkan Munadi (2005) dalam Alfiana (2010), suatu perangkat dasar Geostatistika untuk visualisasi dan pemodelan dikenal sebagai Semivariogram. Semivariogram digunakan untuk menentukan jarak dimana nilai-nilai data pengamatan menjadi tidak saling bergantung atau tidak ada korelasinya. Semivariogram Eksperimental merupakan Semivariogram yang didapatkan berdasarkan nilai pengamatan dan dihitung menggunakan penghitungan sebagai berikut (Isaaks dan Srivastava, 1989).

Berdasarkan Gambar 1 maka dapat dilihat masing-masing properti dari Semivariogram. Nugget effect adalah intersep antara Semivariogram dengan sumbu vertikal. Nugget effect dapat dipengaruhi oleh alat pengukur yang tidak akurat ataupun jarak yang diambil antar pasangan pengamatan tidak tepat. Sill merupakan nilai dari ketika Semivariogram mencapai kondisi konvergen. Semakin tinggi nilai sill maka varians dari estimasi akan semakin besar. Indikasi kondisi spasial juga dapat dilihat berdasarkan rasio antara sill dan nugget effect. Jika rasio mendekati nilai satu maka dapat dikatakan bahwa pengamatan tersebut tidak memiliki dependensi antar ruang atau jarak tertentu.
.jpg)
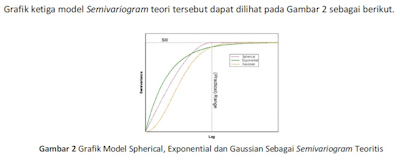
Berdasarkan Semivariogram Eksperimental maka akan dicocokkan dengan model Semivariogram Teoritis dan pada umumnya model Semivariogram Teoritis yang digunakan adalah model linear. Beberapa contoh SemivariogramTeoritis adalah model spherical, exponential dan gaussian (Weckernagel, 1995). Model Spherical ditunjukkan oleh persamaan sebagai berikut.
.jpg)
Pada model Exponential terjadi peningkatan dalam Semivariogram yang sangat curam dan mencapai nilai sill secara asimtotik dan dirumuskan sebagai berikut.
.jpg)
Model gaussian merupakan bentuk kuadrat dari eksponensial sehingga menghasilkan bentuk parabolik pada jarak yang dekat dan dapat dirumuskan sebagai berikut.

Teknik interpolasi yang dikenal dalam Geostatistika yaitu Kriging. Metode ini awalnya digunakan dalam industri pertambangan untuk mengetahui nilai pengamatan pada titik yang belum diambil sampelnya. Krigingmembutuhkan model spasial statistika yang biasa disebut Variogram. Data input untuk metode ini diboboti berdasarkan model Semivariogram, parameter yang diamati dan juga jumlah sampelnya. Semivariogram yang baik akan memberikan estimasi yang baik pula pada metode Kriging. Metode Kriging sederhana adalah metode linier seperti Ordinary Kriging, Universal Kriging, Kriging with External Drift dan yang lainnya. Sebagai contoh, persamaan estimator dari metode Universal Kriging adalah sebagai berikut :
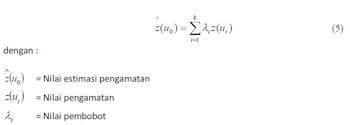

Untuk memudahkan pemahaman maka kita dapat cermati studi kasus sederhana berikut.
- Suatu perusahaan Asuransi Jiwa XYZ ingin mengetahui morbiditas penyakit tertentu pada Kota C. Namun diketahui ternyata belum tersedia penelitian mengenai morbiditas penyakit tersebut di Kota C.
- Kota C berbatasan langsung dengan Kota A, B, D dan E dimana pada keempat kota tersebut nilai morbiditasnya diketahui. Diasumsikan nilai morbiditas penyakit di Kota C merupakan kasus spasial sehingga berkaitan dengan data pada keempat kota tersebut.
- Melakukan penghitungan Semivariogram Eksperimental menggunakan data morbiditas yang tersedia. Lalu didapatkan nilai Semivariogram Eksperimental dan digambarkan dalam grafik.
- Melakukan analisis Semivariogaram Teoritis dengan membuat grafik Semivariogram Teoritis agar didapatkan tiap properti Semivariogramnya. Selanjutnya dipilih model Semivariogram Teoritis terbaik berdasarkan bentuk visual, nilai MSE dan properti Semivariogram.
- Parameter yang dihasilkan Semivariogram Teoritis digunakan untuk menghitung pembobot Kriging.
- Menghitung estimasi morbiditas penyakit tersebut pada Kota C dengan menggunakan persamaan (5) diatas yaitu menggunakan data morbiditas yang tersedia dan pembobot Kriging.
Memang pada umumnya analisa Geostatistika digunakan pada studi kasus pertambangan, lingkungan dan iklim. Oleh karena itu Geostatisika lebih familiar diterapkan pada Asuransi Kerugian. Namun beberapa tahun belakangan ini terdapat publikasi penelitian mengenai aplikasi Geostatistika dalam industri Asuransi Jiwa yang dilakukan oleh Debon (2009) dengan judul “A Geostatistical Approach for Dynamic Table Life”. Selain itu Christiansen (2014) juga menggunakan pendekatan Geostatistika dalam jurnalnya yang berjudul “Differences in European Mortality Rates: A Geometric Approach on the Age-Period Plane”. Kedua jurnal tersebut diselesaikan masing-masing di Spanyol dan Jerman. Mengingat analisa Geostatistika dalam asuransi jiwa di Indonesia belum terlalu banyak dilakukan maka ulasan mendalam mengenai kedua jurnal tersebut akan dibahas pada kesempatan berikutnya. (Rafsan)
Sumber:
- Alfiana, A.N. 2010. Metode Ordinary Kriging pada Geostatistika [Skripsi].
- Christiansen, M.C. dkk. 2014. Differences in European Mortality Rates: A Geometric Approach on the Age-Period Plane
- Debon, A. dkk. 2009. A Geostatistical Approach for Dynamic Table Life
- saaks, H.E. dan Srivastava, R.M. 1989. Applied Geostatistics.
- Weckernagel, H. 1995. Multivariate Geostatistics.
*********
Penulis





 23087
23087



 10 Dec 2016
10 Dec 2016 21170 kali
21170 kali





